[This work is based on this course: Data Science for Business | 6 Real-world Case Studies.]
We have a large dataset of a Bank. The sample dataset summarizes the usage behavior of about 9000 active credit card holders during last 6 months.
The marketing team wants to launch an advertising campaign by segmenting its customers into 3 different groups.
Data Dictionary for Credit Card dataset:
- CUSTID: Identification of Credit Card holder (Categorical)
- BALANCE: Balance amount left in their account to make purchases
- BALANCEFREQUENCY: How frequently the Balance is updated, score between 0 and 1 (1 = frequently updated, 0 = not frequently updated)
- PURCHASES: Amount of purchases made from account
- ONEOFFPURCHASES: Maximum purchase amount done in one-go
- INSTALLMENTSPURCHASES: Amount of purchase done in installment
- CASHADVANCE: Cash in advance given by the user
- PURCHASESFREQUENCY: How frequently the Purchases are being made, score between 0 and 1 (1 = frequently purchased, 0 = not frequently purchased)
- ONEOFFPURCHASESFREQUENCY: How frequently Purchases are happening in one-go (1 = frequently purchased, 0 = not frequently purchased)
- PURCHASESINSTALLMENTSFREQUENCY: How frequently purchases in installments are being done (1 = frequently done, 0 = not frequently done)
- CASHADVANCEFREQUENCY: How frequently the cash in advance being paid
- CASHADVANCETRX: Number of Transactions made with "Cash in Advanced"
- PURCHASESTRX: Numbe of purchase transactions made
- CREDITLIMIT: Limit of Credit Card for user
- PAYMENTS: Amount of Payment done by user
- MINIMUM_PAYMENTS: Minimum amount of payments made by user
- PRCFULLPAYMENT: Percent of full payment paid by user
- TENURE: Tenure of credit card service for user
Data Source: Credit Card Dataset
1 – Import libraries and dataset
import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt from sklearn.preprocessing import StandardScaler, normalize from sklearn.cluster import KMeans from sklearn.decomposition import PCA
df = pd.read_csv("Marketing_data.csv")
df
| CUST_ID | BALANCE | BALANCE_FREQUENCY | PURCHASES | ONEOFF_PURCHASES | INSTALLMENTS_PURCHASES | CASH_ADVANCE | PURCHASES_FREQUENCY | ONEOFF_PURCHASES_FREQUENCY | PURCHASES_INSTALLMENTS_FREQUENCY | CASH_ADVANCE_FREQUENCY | CASH_ADVANCE_TRX | PURCHASES_TRX | CREDIT_LIMIT | PAYMENTS | MINIMUM_PAYMENTS | PRC_FULL_PAYMENT | TENURE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | C10001 | 40.900749 | 0.818182 | 95.40 | 0.00 | 95.40 | 0.000000 | 0.166667 | 0.000000 | 0.083333 | 0.000000 | 0 | 2 | 1000.0 | 201.802084 | 139.509787 | 0.000000 | 12 |
| 1 | C10002 | 3202.467416 | 0.909091 | 0.00 | 0.00 | 0.00 | 6442.945483 | 0.000000 | 0.000000 | 0.000000 | 0.250000 | 4 | 0 | 7000.0 | 4103.032597 | 1072.340217 | 0.222222 | 12 |
| 2 | C10003 | 2495.148862 | 1.000000 | 773.17 | 773.17 | 0.00 | 0.000000 | 1.000000 | 1.000000 | 0.000000 | 0.000000 | 0 | 12 | 7500.0 | 622.066742 | 627.284787 | 0.000000 | 12 |
| 3 | C10004 | 1666.670542 | 0.636364 | 1499.00 | 1499.00 | 0.00 | 205.788017 | 0.083333 | 0.083333 | 0.000000 | 0.083333 | 1 | 1 | 7500.0 | 0.000000 | NaN | 0.000000 | 12 |
| 4 | C10005 | 817.714335 | 1.000000 | 16.00 | 16.00 | 0.00 | 0.000000 | 0.083333 | 0.083333 | 0.000000 | 0.000000 | 0 | 1 | 1200.0 | 678.334763 | 244.791237 | 0.000000 | 12 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 8945 | C19186 | 28.493517 | 1.000000 | 291.12 | 0.00 | 291.12 | 0.000000 | 1.000000 | 0.000000 | 0.833333 | 0.000000 | 0 | 6 | 1000.0 | 325.594462 | 48.886365 | 0.500000 | 6 |
| 8946 | C19187 | 19.183215 | 1.000000 | 300.00 | 0.00 | 300.00 | 0.000000 | 1.000000 | 0.000000 | 0.833333 | 0.000000 | 0 | 6 | 1000.0 | 275.861322 | NaN | 0.000000 | 6 |
| 8947 | C19188 | 23.398673 | 0.833333 | 144.40 | 0.00 | 144.40 | 0.000000 | 0.833333 | 0.000000 | 0.666667 | 0.000000 | 0 | 5 | 1000.0 | 81.270775 | 82.418369 | 0.250000 | 6 |
| 8948 | C19189 | 13.457564 | 0.833333 | 0.00 | 0.00 | 0.00 | 36.558778 | 0.000000 | 0.000000 | 0.000000 | 0.166667 | 2 | 0 | 500.0 | 52.549959 | 55.755628 | 0.250000 | 6 |
| 8949 | C19190 | 372.708075 | 0.666667 | 1093.25 | 1093.25 | 0.00 | 127.040008 | 0.666667 | 0.666667 | 0.000000 | 0.333333 | 2 | 23 | 1200.0 | 63.165404 | 88.288956 | 0.000000 | 6 |
df.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 8950 entries, 0 to 8949 Data columns (total 18 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 CUST_ID 8950 non-null object 1 BALANCE 8950 non-null float64 2 BALANCE_FREQUENCY 8950 non-null float64 3 PURCHASES 8950 non-null float64 4 ONEOFF_PURCHASES 8950 non-null float64 5 INSTALLMENTS_PURCHASES 8950 non-null float64 6 CASH_ADVANCE 8950 non-null float64 7 PURCHASES_FREQUENCY 8950 non-null float64 8 ONEOFF_PURCHASES_FREQUENCY 8950 non-null float64 9 PURCHASES_INSTALLMENTS_FREQUENCY 8950 non-null float64 10 CASH_ADVANCE_FREQUENCY 8950 non-null float64 11 CASH_ADVANCE_TRX 8950 non-null int64 12 PURCHASES_TRX 8950 non-null int64 13 CREDIT_LIMIT 8949 non-null float64 14 PAYMENTS 8950 non-null float64 15 MINIMUM_PAYMENTS 8637 non-null float64 16 PRC_FULL_PAYMENT 8950 non-null float64 17 TENURE 8950 non-null int64 dtypes: float64(14), int64(3), object(1) memory usage: 1.2+ MB
df.describe()
| BALANCE | BALANCE_FREQUENCY | PURCHASES | ONEOFF_PURCHASES | INSTALLMENTS_PURCHASES | CASH_ADVANCE | PURCHASES_FREQUENCY | ONEOFF_PURCHASES_FREQUENCY | PURCHASES_INSTALLMENTS_FREQUENCY | CASH_ADVANCE_FREQUENCY | CASH_ADVANCE_TRX | PURCHASES_TRX | CREDIT_LIMIT | PAYMENTS | MINIMUM_PAYMENTS | PRC_FULL_PAYMENT | TENURE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 8950.000000 | 8950.000000 | 8950.000000 | 8950.000000 | 8950.000000 | 8950.000000 | 8950.000000 | 8950.000000 | 8950.000000 | 8950.000000 | 8950.000000 | 8950.000000 | 8949.000000 | 8950.000000 | 8637.000000 | 8950.000000 | 8950.000000 |
| mean | 1564.474828 | 0.877271 | 1003.204834 | 592.437371 | 411.067645 | 978.871112 | 0.490351 | 0.202458 | 0.364437 | 0.135144 | 3.248827 | 14.709832 | 4494.449450 | 1733.143852 | 864.206542 | 0.153715 | 11.517318 |
| std | 2081.531879 | 0.236904 | 2136.634782 | 1659.887917 | 904.338115 | 2097.163877 | 0.401371 | 0.298336 | 0.397448 | 0.200121 | 6.824647 | 24.857649 | 3638.815725 | 2895.063757 | 2372.446607 | 0.292499 | 1.338331 |
| min | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 50.000000 | 0.000000 | 0.019163 | 0.000000 | 6.000000 |
| 25% | 128.281915 | 0.888889 | 39.635000 | 0.000000 | 0.000000 | 0.000000 | 0.083333 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 1600.000000 | 383.276166 | 169.123707 | 0.000000 | 12.000000 |
| 50% | 873.385231 | 1.000000 | 361.280000 | 38.000000 | 89.000000 | 0.000000 | 0.500000 | 0.083333 | 0.166667 | 0.000000 | 0.000000 | 7.000000 | 3000.000000 | 856.901546 | 312.343947 | 0.000000 | 12.000000 |
| 75% | 2054.140036 | 1.000000 | 1110.130000 | 577.405000 | 468.637500 | 1113.821139 | 0.916667 | 0.300000 | 0.750000 | 0.222222 | 4.000000 | 17.000000 | 6500.000000 | 1901.134317 | 825.485459 | 0.142857 | 12.000000 |
| max | 19043.138560 | 1.000000 | 49039.570000 | 40761.250000 | 22500.000000 | 47137.211760 | 1.000000 | 1.000000 | 1.000000 | 1.500000 | 123.000000 | 358.000000 | 30000.000000 | 50721.483360 | 76406.207520 | 1.000000 | 12.000000 |
- The average balance is $1564.
- The balance frequency is quite often updated, on average ~0.9 (frequently updated).
- The average of purchases is $1000.
- The average of maximum purchase amount done in one-go is ~$600.
- The average of th frequently of purchases is ~0.5.
- On the whole, the average of ONEOFF_PURCHASES_FREQUENCY, PURCHASES_INSTALLMENTS_FREQUENCY and CASH_ADVANCE_FREQUENCY are low.
- The average of the limit of Credit Card for user is ~$4500
- Percent of full payment paid by user is 15%
- Tenure of credit card service for user is 11 years.
Let’s go to figure out who has made a purchase of $40761 in one-go:
df[df["ONEOFF_PURCHASES"] == 40761.25]
| CUST_ID | BALANCE | BALANCE_FREQUENCY | PURCHASES | ONEOFF_PURCHASES | INSTALLMENTS_PURCHASES | CASH_ADVANCE | PURCHASES_FREQUENCY | ONEOFF_PURCHASES_FREQUENCY | PURCHASES_INSTALLMENTS_FREQUENCY | CASH_ADVANCE_FREQUENCY | CASH_ADVANCE_TRX | PURCHASES_TRX | CREDIT_LIMIT | PAYMENTS | MINIMUM_PAYMENTS | PRC_FULL_PAYMENT | TENURE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 550 | C10574 | 11547.52001 | 1.0 | 49039.57 | 40761.25 | 8278.32 | 558.166886 | 1.0 | 1.0 | 0.916667 | 0.083333 | 1 | 101 | 22500.0 | 46930.59824 | 2974.069421 | 0.25 | 12 |
This client did 123 number of Transactions made with “Cash in Advanced”.
2 – Dataset Visualization
2.1 – First we’re going to check if we have missing values:
sns.heatmap(df.isnull(), yticklabels=False, cbar = False, cmap = "Blues")

df.isnull().sum()
CUST_ID 0 BALANCE 0 BALANCE_FREQUENCY 0 PURCHASES 0 ONEOFF_PURCHASES 0 INSTALLMENTS_PURCHASES 0 CASH_ADVANCE 0 PURCHASES_FREQUENCY 0 ONEOFF_PURCHASES_FREQUENCY 0 PURCHASES_INSTALLMENTS_FREQUENCY 0 CASH_ADVANCE_FREQUENCY 0 CASH_ADVANCE_TRX 0 PURCHASES_TRX 0 CREDIT_LIMIT 1 PAYMENTS 0 MINIMUM_PAYMENTS 313 PRC_FULL_PAYMENT 0 TENURE 0 dtype: int64
– We fill the missing values with the average of ‘MINIMUM_PAYMENT’ and ‘CREDIT_LIMIT’:
df.loc[(df['MINIMUM_PAYMENTS'].isnull() == True), 'MINIMUM_PAYMENTS'] = df['MINIMUM_PAYMENTS'].mean() df.loc[(df['CREDIT_LIMIT'].isnull() == True), 'CREDIT_LIMIT'] = df['CREDIT_LIMIT'].mean()
2.2 – Second we’re going to check if we have duplicate values in our data:
df.duplicated().sum()
0
sns.heatmap(df.isnull(), yticklabels=False, cbar = False, cmap = "Blues")

– We can remove CustomerID because it doesn’t useful:
df.drop("CUST_ID", axis = 1, inplace=True)
df.head()
| BALANCE | BALANCE_FREQUENCY | PURCHASES | ONEOFF_PURCHASES | INSTALLMENTS_PURCHASES | CASH_ADVANCE | PURCHASES_FREQUENCY | ONEOFF_PURCHASES_FREQUENCY | PURCHASES_INSTALLMENTS_FREQUENCY | CASH_ADVANCE_FREQUENCY | CASH_ADVANCE_TRX | PURCHASES_TRX | CREDIT_LIMIT | PAYMENTS | MINIMUM_PAYMENTS | PRC_FULL_PAYMENT | TENURE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 40.900749 | 0.818182 | 95.40 | 0.00 | 95.4 | 0.000000 | 0.166667 | 0.000000 | 0.083333 | 0.000000 | 0 | 2 | 1000.0 | 201.802084 | 139.509787 | 0.000000 | 12 |
| 1 | 3202.467416 | 0.909091 | 0.00 | 0.00 | 0.0 | 6442.945483 | 0.000000 | 0.000000 | 0.000000 | 0.250000 | 4 | 0 | 7000.0 | 4103.032597 | 1072.340217 | 0.222222 | 12 |
| 2 | 2495.148862 | 1.000000 | 773.17 | 773.17 | 0.0 | 0.000000 | 1.000000 | 1.000000 | 0.000000 | 0.000000 | 0 | 12 | 7500.0 | 622.066742 | 627.284787 | 0.000000 | 12 |
| 3 | 1666.670542 | 0.636364 | 1499.00 | 1499.00 | 0.0 | 205.788017 | 0.083333 | 0.083333 | 0.000000 | 0.083333 | 1 | 1 | 7500.0 | 0.000000 | 864.206542 | 0.000000 | 12 |
| 4 | 817.714335 | 1.000000 | 16.00 | 16.00 | 0.0 | 0.000000 | 0.083333 | 0.083333 | 0.000000 | 0.000000 | 0 | 1 | 1200.0 | 678.334763 | 244.791237 | 0.000000 | 12 |
n = len(df.columns) n
17
df.columns
Index(['BALANCE', 'BALANCE_FREQUENCY', 'PURCHASES', 'ONEOFF_PURCHASES',
'INSTALLMENTS_PURCHASES', 'CASH_ADVANCE', 'PURCHASES_FREQUENCY',
'ONEOFF_PURCHASES_FREQUENCY', 'PURCHASES_INSTALLMENTS_FREQUENCY',
'CASH_ADVANCE_FREQUENCY', 'CASH_ADVANCE_TRX', 'PURCHASES_TRX',
'CREDIT_LIMIT', 'PAYMENTS', 'MINIMUM_PAYMENTS', 'PRC_FULL_PAYMENT',
'TENURE'],
dtype='object')
### The Kernel Density Estimate:
plt.figure(figsize = (10, 50))
for i in range(n):
plt.subplot(n, 1, i+1)
sns.distplot(df[df.columns[i]], kde_kws = {"color": "b", "lw": 3, "label": "KDE", 'bw': 0.2}, hist_kws={"color": "g"})
plt.title(df.columns[i])
plt.tight_layout()
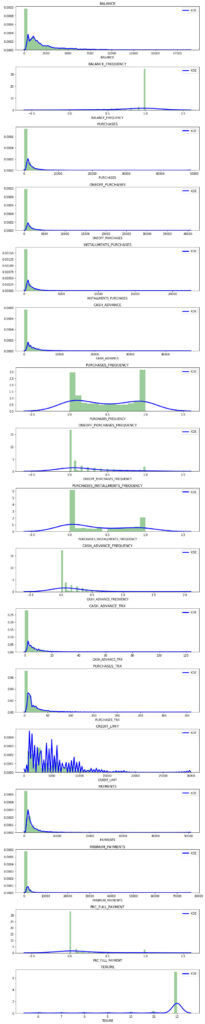
Correlation between variables:
correlations = df.corr() f, ax = plt.subplots(figsize = (20,20)) sns.heatmap(correlations, annot = True)
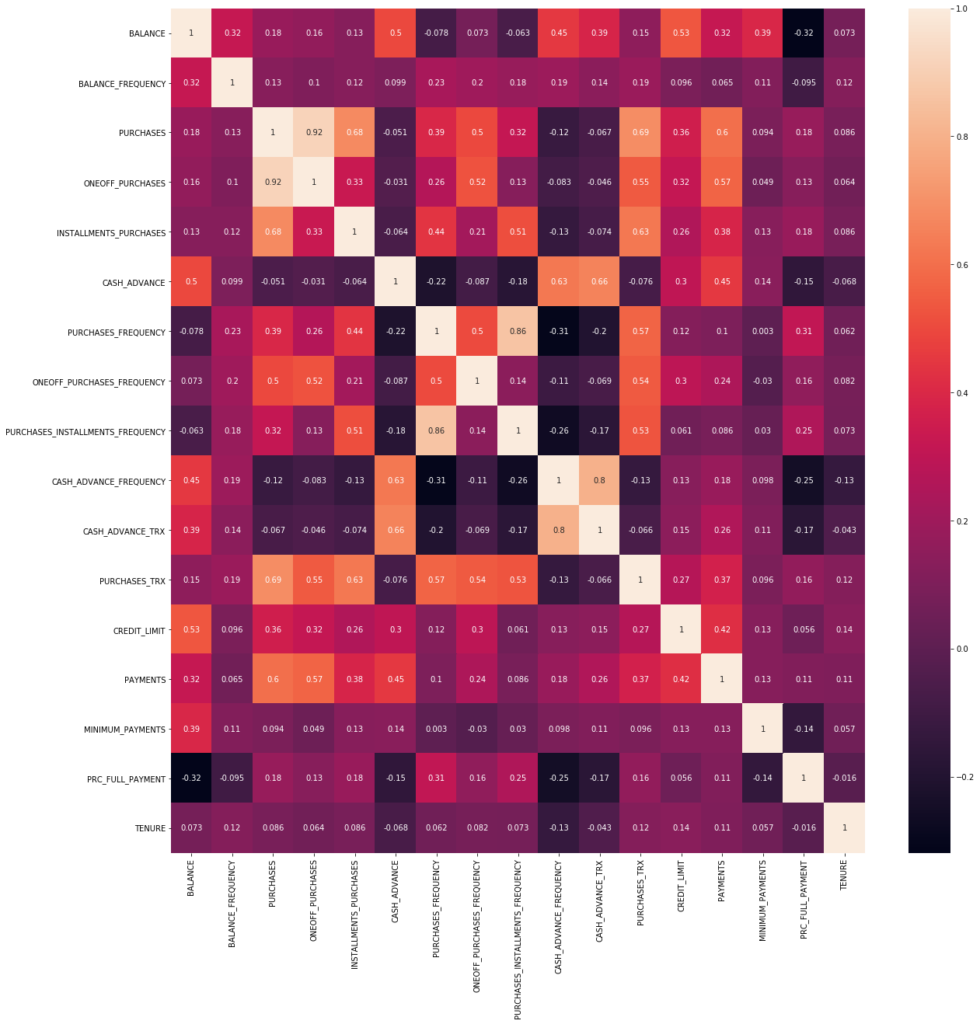
- There is a correlation between PURCHASES and ONEOFF_PURCHASES and INSTALMENT_PURCHASES variables.
- We also can see a tend between PURCHASES with CREDIT_LIMIT and PAYMENTS.
- High correlation between PURCHASES_FREQUENCY and PURCHASES_INSTALLMENT_FREQUENCY too.
3 – Finding the optimal number of clusters using ‘The Elbow Method’
- ‘The Elbow Method’ consists of plotting the explained variation as a function of the number of clusters, and picking the elbow of the curve as the number of clusters to use. This method has been designed to help to find the appropriate number of clusters in our dataset.
- If the line graph looks like an "arm", then the "elbow" on the arm is the value of k. This k will be our number of clusters.
Source:
- https://en.wikipedia.org/wiki/Elbow_method_(clustering)
- https://www.geeksforgeeks.org/elbow-method-for-optimal-value-of-k-in-kmeans/
First let’s start scaling our dataset. In this way no varaible will stand out.
scaler = StandardScaler() df_scaled = scaler.fit_transform(df) df_scaled.shape
(8950, 17)
df_scaled
array([[-0.73198937, -0.24943448, -0.42489974, ..., -0.31096755,
-0.52555097, 0.36067954],
[ 0.78696085, 0.13432467, -0.46955188, ..., 0.08931021,
0.2342269 , 0.36067954],
[ 0.44713513, 0.51808382, -0.10766823, ..., -0.10166318,
-0.52555097, 0.36067954],
...,
[-0.7403981 , -0.18547673, -0.40196519, ..., -0.33546549,
0.32919999, -4.12276757],
[-0.74517423, -0.18547673, -0.46955188, ..., -0.34690648,
0.32919999, -4.12276757],
[-0.57257511, -0.88903307, 0.04214581, ..., -0.33294642,
-0.52555097, -4.12276757]])
– We apply the elbow method:
scores_1 = []
range_values = range(1, 20)
for i in range_values:
kmeans = KMeans(n_clusters = i)
kmeans.fit(df_scaled)
scores_1.append(kmeans.inertia_) #WCSS
plt.plot(range_values, scores_1, 'bx-')
plt.title("Encontrar el número óptimo de Clusters")
plt.xlabel("Clusters")
plt.ylabel("WCSS(k)")
plt.show()
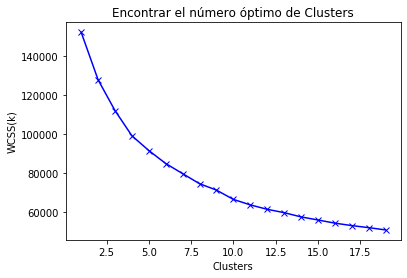
- The tendency of the "arm" tends to smooth the curve out (our "elbow") about cluster’s number 4.
- The values aren’t reduced a linear tendency until the 8th cluster. We choose this number.
4 – K-Means Method
kmeans = KMeans(8) kmeans.fit(df_scaled) labels = kmeans.labels_ labels
array([1, 3, 6, ..., 7, 7, 7], dtype=int32)
Cluster number of each point.
kmeans.cluster_centers_.shape #we have 8 baricentros con las 17 variables(features)
(8, 17)
We have 8 barycenters and 17 features.
cluster_centers = pd.DataFrame(data = kmeans.cluster_centers_, columns=[df.columns]) cluster_centers
| BALANCE | BALANCE_FREQUENCY | PURCHASES | ONEOFF_PURCHASES | INSTALLMENTS_PURCHASES | CASH_ADVANCE | PURCHASES_FREQUENCY | ONEOFF_PURCHASES_FREQUENCY | PURCHASES_INSTALLMENTS_FREQUENCY | CASH_ADVANCE_FREQUENCY | CASH_ADVANCE_TRX | PURCHASES_TRX | CREDIT_LIMIT | PAYMENTS | MINIMUM_PAYMENTS | PRC_FULL_PAYMENT | TENURE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -0.361746 | 0.332427 | -0.034919 | -0.242534 | 0.362821 | -0.363296 | 0.993026 | -0.383768 | 1.205252 | -0.473549 | -0.360250 | 0.189465 | -0.261298 | -0.214984 | -0.030438 | 0.313451 | 0.256258 |
| 1 | 0.012363 | 0.404002 | -0.357001 | -0.241611 | -0.400131 | -0.094194 | -0.852812 | -0.394335 | -0.754538 | 0.103185 | -0.028265 | -0.481551 | -0.303354 | -0.249373 | -0.011771 | -0.455386 | 0.273280 |
| 2 | 1.845310 | 0.340595 | 12.297201 | 12.823670 | 5.516158 | 0.272530 | 1.043177 | 2.145028 | 0.896761 | -0.380373 | -0.109730 | 4.556136 | 3.185151 | 9.047799 | 1.030898 | 1.222264 | 0.298409 |
| 3 | 1.686129 | 0.393025 | -0.217205 | -0.155325 | -0.228287 | 2.009008 | -0.470733 | -0.207959 | -0.411112 | 1.913538 | 1.919868 | -0.265613 | 1.029379 | 0.818956 | 0.552301 | -0.390101 | 0.071370 |
| 4 | -0.701258 | -2.140285 | -0.310336 | -0.234722 | -0.302444 | -0.322272 | -0.554827 | -0.441460 | -0.440553 | -0.521236 | -0.376356 | -0.419376 | -0.176011 | -0.202115 | -0.256800 | 0.283165 | 0.198977 |
| 5 | 1.039400 | 0.464856 | 2.504641 | 1.808428 | 2.599812 | -0.161205 | 1.164502 | 1.562982 | 1.272947 | -0.286097 | -0.150710 | 3.134487 | 1.297181 | 1.439786 | 0.560536 | 0.253915 | 0.337460 |
| 6 | -0.132975 | 0.400605 | 0.541559 | 0.671442 | 0.046770 | -0.331239 | 0.980011 | 1.904813 | 0.171671 | -0.412879 | -0.329926 | 0.618406 | 0.434597 | 0.144731 | -0.158053 | 0.444399 | 0.268773 |
| 7 | -0.336228 | -0.347383 | -0.287908 | -0.214195 | -0.286875 | 0.067425 | -0.201713 | -0.285924 | -0.224146 | 0.307084 | 0.000231 | -0.387540 | -0.563820 | -0.392784 | -0.209266 | 0.014243 | -3.202809 |
The inverse transformation of scaling is applied to understand better this values.
cluster_centers = scaler.inverse_transform(cluster_centers) cluster_centers = pd.DataFrame(data = cluster_centers, columns=[df.columns]) cluster_centers
| BALANCE | BALANCE_FREQUENCY | PURCHASES | ONEOFF_PURCHASES | INSTALLMENTS_PURCHASES | CASH_ADVANCE | PURCHASES_FREQUENCY | ONEOFF_PURCHASES_FREQUENCY | PURCHASES_INSTALLMENTS_FREQUENCY | CASH_ADVANCE_FREQUENCY | CASH_ADVANCE_TRX | PURCHASES_TRX | CREDIT_LIMIT | PAYMENTS | MINIMUM_PAYMENTS | PRC_FULL_PAYMENT | TENURE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 811.530431 | 0.956020 | 928.599272 | 189.879812 | 739.162116 | 217.022499 | 0.888900 | 0.087972 | 0.843436 | 0.040382 | 0.790387 | 19.419227 | 3543.741428 | 1110.786328 | 793.273098 | 0.245394 | 11.860258 |
| 1 | 1590.206589 | 0.972975 | 240.466411 | 191.411976 | 49.234195 | 781.342922 | 0.148076 | 0.084820 | 0.064565 | 0.155793 | 3.055939 | 2.740283 | 3390.725269 | 1011.232951 | 836.775777 | 0.020522 | 11.883037 |
| 2 | 5405.330935 | 0.957955 | 27276.363750 | 21877.102917 | 5399.260833 | 1550.378389 | 0.909028 | 0.842361 | 0.720833 | 0.059028 | 2.500000 | 127.958333 | 16083.333333 | 27925.634496 | 3266.671038 | 0.511206 | 11.916667 |
| 3 | 5074.010044 | 0.970375 | 539.143482 | 334.629072 | 204.630871 | 5191.855751 | 0.301422 | 0.140419 | 0.201051 | 0.518063 | 16.350515 | 8.107675 | 8239.753202 | 4103.940565 | 2151.320463 | 0.039617 | 11.612829 |
| 4 | 104.865352 | 0.370257 | 340.166450 | 202.846306 | 137.571031 | 303.051343 | 0.267672 | 0.070762 | 0.189350 | 0.030840 | 0.680473 | 4.285714 | 3854.048558 | 1148.040394 | 265.744196 | 0.236535 | 11.783601 |
| 5 | 3727.898336 | 0.987391 | 6354.408362 | 3594.057458 | 2762.045819 | 640.817196 | 0.957721 | 0.668725 | 0.870339 | 0.077893 | 2.220339 | 92.621469 | 9214.124294 | 5901.184611 | 2170.512276 | 0.227980 | 11.968927 |
| 6 | 1287.698840 | 0.972170 | 2160.255009 | 1706.894046 | 453.360963 | 284.247254 | 0.883676 | 0.770700 | 0.432664 | 0.052523 | 0.997326 | 30.081105 | 6075.692756 | 2152.127140 | 495.870743 | 0.283694 | 11.877005 |
| 7 | 864.645308 | 0.794979 | 388.085586 | 236.917416 | 151.649711 | 1120.263874 | 0.409393 | 0.117161 | 0.275356 | 0.196595 | 3.250401 | 5.077047 | 2443.040850 | 596.072587 | 376.521919 | 0.157880 | 7.231140 |
- First Cluster of Clients (Transactors): Those are the clients who pay the least amount of interest charges and they are very careful with their money. The lowest balance ($ 104) and cash advance ($ 303). Full payment = 23%.
- Second Cluster of clients (Revolvers): They use the credit card as a loan (the most lucrative sector): higher balance (
$ 5000) and cash advance (~ $ 5000), low purchase frequency, high advance frequency cash (0.5), high cash advance transactions (16`) and low payment percentage (3%). - Third Cluster of Clients (VIP / Prime): High credit limit
$ 16Kand higher percentage of full payment, goal to increase credit limit and increase spending habits. - Fourth Cluster of Clients (low tenure): They are clients with low seniority (7 years), low balance.
labels.shape
(8950,)
labels.min()
0
labels.max()
7
– We can also make predictions:
y_kmeans = kmeans.fit_predict(df_scaled) y_kmeans
array([0, 2, 5, ..., 6, 6, 6], dtype=int32)
Let’s go to concatenate clusters’ labels with the original dataset. In this way we can see which cluster each observation belongs to:
df_cluster = pd.concat([df, pd.DataFrame({'cluster': labels})], axis = 1)
df_cluster.head()
| BALANCE | BALANCE_FREQUENCY | PURCHASES | ONEOFF_PURCHASES | INSTALLMENTS_PURCHASES | CASH_ADVANCE | PURCHASES_FREQUENCY | ONEOFF_PURCHASES_FREQUENCY | PURCHASES_INSTALLMENTS_FREQUENCY | CASH_ADVANCE_FREQUENCY | CASH_ADVANCE_TRX | PURCHASES_TRX | CREDIT_LIMIT | PAYMENTS | MINIMUM_PAYMENTS | PRC_FULL_PAYMENT | TENURE | cluster | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 40.900749 | 0.818182 | 95.40 | 0.00 | 95.4 | 0.000000 | 0.166667 | 0.000000 | 0.083333 | 0.000000 | 0 | 2 | 1000.0 | 201.802084 | 139.509787 | 0.000000 | 12 | 1 |
| 1 | 3202.467416 | 0.909091 | 0.00 | 0.00 | 0.0 | 6442.945483 | 0.000000 | 0.000000 | 0.000000 | 0.250000 | 4 | 0 | 7000.0 | 4103.032597 | 1072.340217 | 0.222222 | 12 | 3 |
| 2 | 2495.148862 | 1.000000 | 773.17 | 773.17 | 0.0 | 0.000000 | 1.000000 | 1.000000 | 0.000000 | 0.000000 | 0 | 12 | 7500.0 | 622.066742 | 627.284787 | 0.000000 | 12 | 6 |
| 3 | 1666.670542 | 0.636364 | 1499.00 | 1499.00 | 0.0 | 205.788017 | 0.083333 | 0.083333 | 0.000000 | 0.083333 | 1 | 1 | 7500.0 | 0.000000 | 864.206542 | 0.000000 | 12 | 1 |
| 4 | 817.714335 | 1.000000 | 16.00 | 16.00 | 0.0 | 0.000000 | 0.083333 | 0.083333 | 0.000000 | 0.000000 | 0 | 1 | 1200.0 | 678.334763 | 244.791237 | 0.000000 | 12 | 1 |
– We visualize histograms for each cluster:
for i in df.columns:
plt.figure(figsize=(35, 5))
for j in range(8):
plt.subplot(1, 8, j+1)
cluster = df_cluster[df_cluster['cluster'] == j]
cluster[i].hist(bins = 20)
plt.title('{} \nCluster {}'.format(i, j))
plt.show()
5 – Principal Component Analysis (PCA)
pca = PCA(n_components = 2) principal_comp = pca.fit_transform(df_scaled) principal_comp
array([[-1.68221922, -1.07645126],
[-1.13829358, 2.50647075],
[ 0.96968292, -0.38350887],
...,
[-0.92620252, -1.81078537],
[-2.33655126, -0.65796865],
[-0.55642498, -0.40046541]])
We’re going to create a dataframe with the two components:
pca_df = pd.DataFrame(data = principal_comp, columns=["pca1", "pca2"]) pca_df.head()
| pca1 | pca2 | |
|---|---|---|
| 0 | -1.682219 | -1.076451 |
| 1 | -1.138294 | 2.506471 |
| 2 | 0.969683 | -0.383509 |
| 3 | -0.873627 | 0.043164 |
| 4 | -1.599433 | -0.688581 |
Let’s go to concatenate clusters’ labels with the principals components’ dataset:
pca_df = pd.concat([pca_df, pd.DataFrame({'cluster':labels})], axis = 1)
pca_df.head()
| pca1 | pca2 | cluster | |
|---|---|---|---|
| 0 | -1.682219 | -1.076451 | 1 |
| 1 | -1.138294 | 2.506471 | 3 |
| 2 | 0.969683 | -0.383509 | 6 |
| 3 | -0.873627 | 0.043164 | 1 |
| 4 | -1.599433 | -0.688581 | 1 |
plt.figure(figsize=(10,10))
ax = sns.scatterplot(x = "pca1", y = "pca2", hue = "cluster", data = pca_df,
palette = ["red", "green", "blue", "pink", "yellow", "gray", "purple", "black"])
plt.show()
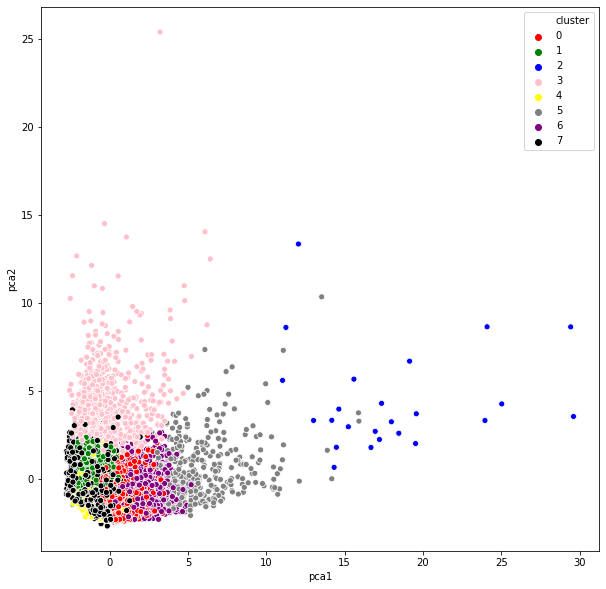
- PCA has reduced our
17dimensions to only2(it must be taken into account the K-means method was applied before the PCA, that’s why some overlapping groups appear). - The pink’s cluster are much more scatted than the rest. While the yellow ones have a lot of information that goes to pca2, or the blue ones (they are grouped around pca1).
- The rest of them are near to
0, which means that they have similar values.
6 – Autoencoders: Neuronal Network to reduce the dimension of our dataset.
AveragePooling2D, MaxPooling2D, Dropout from tensorflow.keras.models import Model, load_model from tensorflow.keras.initializers import glorot_uniform from keras.optimizers import SGD #stochastic grade descent #Compress all info into 7 dimensions. encoding_dim = 7 input_df = Input(shape = (17, ))
Let’s go to create de layers:
#The ReLU's activation function (Rectified Linear Unit) x = Dense(encoding_dim, activation = 'relu')(input_df) #3 hidden layers. # Glorot normal inicializador (Xavier normal initializer) it takes a random samples of a truncated normal distribution x = Dense(500, activation = 'relu', kernel_initializer = 'glorot_uniform')(x) x = Dense(500, activation = 'relu', kernel_initializer = 'glorot_uniform')(x) x = Dense(2000, activation = 'relu', kernel_initializer = 'glorot_uniform')(x) #We finally encode everything to only 10 neurons (the info in the encoder layer) encoded = Dense(10, activation = 'relu', kernel_initializer = 'glorot_uniform')(x) #decompress (it does't have to be symmetrical, we avoid multicollinearity) x = Dense(2000, activation = 'relu', kernel_initializer = 'glorot_uniform')(encoded) x = Dense(500, activation = 'relu', kernel_initializer = 'glorot_uniform')(x) #we finally decode everything to the initial 17 variables decoded = Dense(17, kernel_initializer = 'glorot_uniform')(x) #we define the autoencoder with the layer model autoencoder = Model(input_df, decoded) autoencoder.compile(optimizer = 'adam', loss = 'mean_squared_error') #we save the compression part, we'll use it later to verify our model encoder = Model(input_df, encoded)
df_scaled.shape
(8950, 17)
autoencoder.summary()
Model: "functional_1" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= input_1 (InputLayer) [(None, 17)] 0 _________________________________________________________________ dense (Dense) (None, 7) 126 _________________________________________________________________ dense_1 (Dense) (None, 500) 4000 _________________________________________________________________ dense_2 (Dense) (None, 500) 250500 _________________________________________________________________ dense_3 (Dense) (None, 2000) 1002000 _________________________________________________________________ dense_4 (Dense) (None, 10) 20010 _________________________________________________________________ dense_5 (Dense) (None, 2000) 22000 _________________________________________________________________ dense_6 (Dense) (None, 500) 1000500 _________________________________________________________________ dense_7 (Dense) (None, 17) 8517 ================================================================= Total params: 2,307,653 Trainable params: 2,307,653 Non-trainable params: 0 _________________________________________________________________
autoencoder.fit(df_scaled, df_scaled, batch_size=128, epochs = 25, verbose = 1)
Epoch 1/25 70/70 [==============================] - 3s 42ms/step - loss: 0.6645 Epoch 2/25 70/70 [==============================] - 3s 37ms/step - loss: 0.3590 Epoch 3/25 70/70 [==============================] - 3s 39ms/step - loss: 0.2527 Epoch 4/25 70/70 [==============================] - 2s 35ms/step - loss: 0.1980 Epoch 5/25 70/70 [==============================] - 2s 35ms/step - loss: 0.1706 Epoch 6/25 70/70 [==============================] - 3s 44ms/step - loss: 0.1584 Epoch 7/25 70/70 [==============================] - 3s 37ms/step - loss: 0.1404 Epoch 8/25 70/70 [==============================] - 3s 40ms/step - loss: 0.1285 Epoch 9/25 70/70 [==============================] - 3s 37ms/step - loss: 0.1284 Epoch 10/25 70/70 [==============================] - 3s 45ms/step - loss: 0.1135 Epoch 11/25 70/70 [==============================] - 3s 45ms/step - loss: 0.1050 Epoch 12/25 70/70 [==============================] - 3s 38ms/step - loss: 0.1013 Epoch 13/25 70/70 [==============================] - 3s 43ms/step - loss: 0.0951 Epoch 14/25 70/70 [==============================] - 3s 40ms/step - loss: 0.0915 Epoch 15/25 70/70 [==============================] - 3s 36ms/step - loss: 0.0897 Epoch 16/25 70/70 [==============================] - 3s 40ms/step - loss: 0.0866 Epoch 17/25 70/70 [==============================] - 3s 39ms/step - loss: 0.0858 Epoch 18/25 70/70 [==============================] - 3s 38ms/step - loss: 0.0830 Epoch 19/25 70/70 [==============================] - 2s 33ms/step - loss: 0.0788 Epoch 20/25 70/70 [==============================] - 2s 35ms/step - loss: 0.0809 Epoch 21/25 70/70 [==============================] - 2s 33ms/step - loss: 0.0763 Epoch 22/25 70/70 [==============================] - 2s 33ms/step - loss: 0.0716 Epoch 23/25 70/70 [==============================] - 2s 33ms/step - loss: 0.0705 Epoch 24/25 70/70 [==============================] - 3s 37ms/step - loss: 0.0675 Epoch 25/25 70/70 [==============================] - 2s 33ms/step - loss: 0.0807 <tensorflow.python.keras.callbacks.History at 0x7fd8cc034250>
We obtain a loss function of 0.0657.
– We save the weights to make the predictions:
autoencoder.save_weights('autoencoder.h5') #.h5 neuronal netwotk standard extension
– We apply the encoder created above (the first half of our network belongs to the encode part) to predict:
pred = encoder.predict(df_scaled) pred.shape
(8950, 10)
We have 10 characteristics. They correspond to half of the neural network (as we can see in the summary above).
Let’s apply K-Means:
scores_2 = []
range_values = range(1,20)
for i in range_values:
kmeans = KMeans(n_clusters = i)
kmeans.fit(pred)
scores_2.append(kmeans.inertia_)
plt.plot(range_values, scores_2, 'bx-')
plt.title("Encontrar el número óptimo de clusters")
plt.xlabel("Número de Clusters")
plt.ylabel("WCSS(k)")
plt.show()
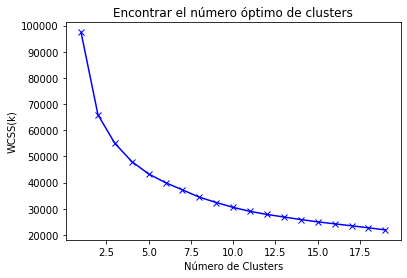
The elbow stabilizes around $k=4$.
We’re going to compare the 2 elbows obtained in this work following different paths:
plt.plot(range_values, scores_1, 'bx-', color = "r") plt.plot(range_values, scores_2, 'bx-', color = "g")
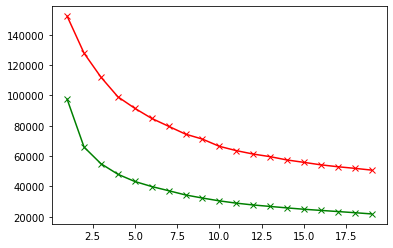
We keep $k=4$
kmeans = KMeans(4) kmeans.fit(pred) labels = kmeans.labels_ y_kmeans = kmeans.fit_predict(pred)
df_cluster_dr = pd.concat([df, pd.DataFrame({'cluster': labels})], axis = 1)
df_cluster_dr.head()
| BALANCE | BALANCE_FREQUENCY | PURCHASES | ONEOFF_PURCHASES | INSTALLMENTS_PURCHASES | CASH_ADVANCE | PURCHASES_FREQUENCY | ONEOFF_PURCHASES_FREQUENCY | PURCHASES_INSTALLMENTS_FREQUENCY | CASH_ADVANCE_FREQUENCY | CASH_ADVANCE_TRX | PURCHASES_TRX | CREDIT_LIMIT | PAYMENTS | MINIMUM_PAYMENTS | PRC_FULL_PAYMENT | TENURE | cluster | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 40.900749 | 0.818182 | 95.40 | 0.00 | 95.4 | 0.000000 | 0.166667 | 0.000000 | 0.083333 | 0.000000 | 0 | 2 | 1000.0 | 201.802084 | 139.509787 | 0.000000 | 12 | 1 |
| 1 | 3202.467416 | 0.909091 | 0.00 | 0.00 | 0.0 | 6442.945483 | 0.000000 | 0.000000 | 0.000000 | 0.250000 | 4 | 0 | 7000.0 | 4103.032597 | 1072.340217 | 0.222222 | 12 | 0 |
| 2 | 2495.148862 | 1.000000 | 773.17 | 773.17 | 0.0 | 0.000000 | 1.000000 | 1.000000 | 0.000000 | 0.000000 | 0 | 12 | 7500.0 | 622.066742 | 627.284787 | 0.000000 | 12 | 0 |
| 3 | 1666.670542 | 0.636364 | 1499.00 | 1499.00 | 0.0 | 205.788017 | 0.083333 | 0.083333 | 0.000000 | 0.083333 | 1 | 1 | 7500.0 | 0.000000 | 864.206542 | 0.000000 | 12 | 0 |
| 4 | 817.714335 | 1.000000 | 16.00 | 16.00 | 0.0 | 0.000000 | 0.083333 | 0.083333 | 0.000000 | 0.000000 | 0 | 1 | 1200.0 | 678.334763 | 244.791237 | 0.000000 | 12 | 1 |
pca = PCA(n_components=2) princ_comp = pca.fit_transform(pred) pca_df = pd.DataFrame(data = princ_comp, columns=["pca1", "pca2"]) pca_df.head()
| pca1 | pca2 | |
|---|---|---|
| 0 | -1.705835 | -0.162720 |
| 1 | 3.051461 | -1.535872 |
| 2 | 0.292494 | 1.344226 |
| 3 | 0.675992 | 0.319985 |
| 4 | -1.705685 | -0.063674 |
pca_df = pd.concat([pca_df, pd.DataFrame({"cluster":labels})], axis = 1)
pca_df
| pca1 | pca2 | cluster | |
|---|---|---|---|
| 0 | -1.705835 | -0.162720 | 1 |
| 1 | 3.051461 | -1.535872 | 0 |
| 2 | 0.292494 | 1.344226 | 0 |
| 3 | 0.675992 | 0.319985 | 0 |
| 4 | -1.705685 | -0.063674 | 1 |
| ... | ... | ... | ... |
| 8945 | -1.279127 | -0.162793 | 1 |
| 8946 | -1.260987 | -0.569104 | 1 |
| 8947 | -1.207046 | -0.294098 | 1 |
| 8948 | -0.051287 | -0.897754 | 1 |
| 8949 | 0.251878 | -0.291193 | 0 |
plt.figure(figsize=(10,10)) ax = sns.scatterplot(x="pca1", y = "pca2", hue="cluster", data = pca_df, palette=["red", "green", "blue", "yellow"]) plt.show()
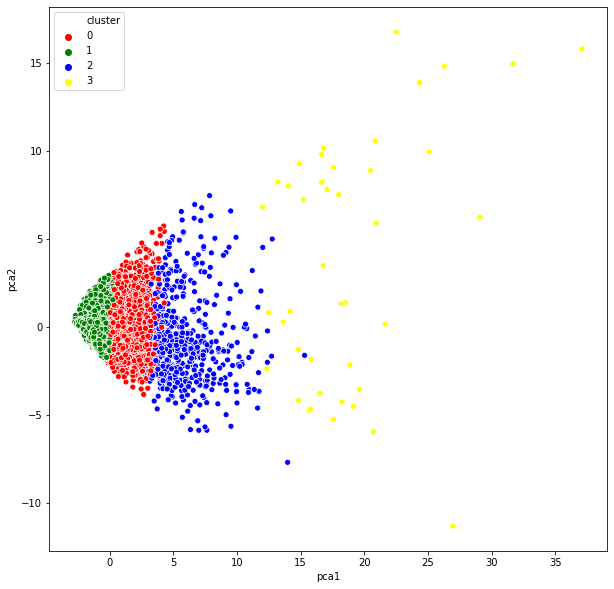
We can see how only with the first principal component (pca1) we could decide which cluster each observation belongs.














