[This work is based on this course: Artificial Intelligence for Business.]

We will configure our own server environment and build an AI that will control the cooling/heating of the server to keep it in an optimal temperature range and at the same time we need to save the maximum energy, thus minimizing costs. Our goal will be to achieve at least 40% energy savings.

1 – Boundary Conditions and program operation

– Parameters:

The average atmospheric temperature for a month.
The optimal range of server temperature: [15ºC, 25ºC].
The minimum server temperature: -25ºC (it doesn’t operate below).
The maximum server temperature: 80ºC (it doesn’t work above).
The minimum number of users on the server: 8.
The maximum number of users on the server: 120.
The maximum number of users on the server that it can up or down per minute: 6.
The minimum data transmission rate on the server: 20.
The maximum data transmission speed on the server: 400.
The maximum data transmission speed that can go up or down per minute: 10.

– Variables:

Server temperature at any time.
Number of users on the server at any time.
Data transmission speed at any minute
AI’s energy expended on the server (to cool or heat it) at any time.
The energy expended by the server’s integrated cooling system that automatically brings the server temperature to the optimal range whenever the server temperature is out of this optimal range.

We are going to make two assumptions to facilitate the work:

First, the server temperature can be approximated by Multiple Linear Regression:

$Server \hspace{2mm} temp. = a_0 + b_1 \cdot atmosph. temp. + b_2 \cdot Num.users + b_3 \cdot data\hspace{2mm} trans.rate$

where $a_0 \in \mathbb R$ , $b_1,b_2,b_3 > 0$

When the atmospheric temperature rieses, the server temperature rises too. The more users are active on the server, the more the server will spend to handle them, and therefore the server temperature will be higher. And finally, the more data is transmitted within the server, the more the server will spend to process it, and therefore the higher the server temperature will be. And for simplicity, we just assume these correlations are linear.

We are going to give values to parameters:

$Server \hspace{2mm} temp. = 0 + 1 \cdot atmosph. temp. + 1.3 \cdot Num.users + 1.3 \cdot data\hspace{2mm} trans.rate$

Second, the energy expended by our system (IA or IRS) that changes the server temperature from $T_t$ to $T_{t+1}$ in a unit of time (1 minute in our problem), it can be approximated again by linear function regression of the absolute change in server temperature:

$E_t=\alpha |\varDelta T_t| + \beta = \alpha |T_{t+1} - T_t| + \beta$

Where:

$E_t$ is the energy expended by the system between $t$ and $t+1$ .
$\varDelta T_t$ is the change of temperature of the system between $t$ and $t+1$ .
$T_t$ and $T_{t+1}$ are the server temperature in $t$ and $t+1$ .
$\alpha >0$ and $\beta \in \mathbb R$ . Although we put them like $\alpha=1$ and $\beta=0$ (for example).

Finnaly we have:

$E_t = |\Delta T_t| = |T_{t+1} - T_t| =$

$= T_{t+1} - T_t$ si $T_{t+1} > T_t$ , (the server heats up)
$= T_t - T_{t+1}$ si $T_{t+1} < T_t$ , (the server gets cold)

How the simulation works:

We are going to simulate a real server and for that the number of users and data transmission speed will fluctuate randomly. AI has to understand how much cooling and heating power it must transfer to server. In this way the program must be able to spend the least energy optimizing its heat transfer.

General operation:

Two possible systems can regulate the server temperature: the AI or the server’s integrated cooling system. The integrated server cooling system is a non- intelligent system. This system will automatically return the server temperature to its optimal temperature. The integrated system(no-IA) works only when IA system not work. If IA is enabled, no-IA is disabled and then the IA updates the server temperature. The IA system is non-deterministic because it predicts what temperatureto set based on the previous parameters.

The IA must spend less energy than the intern cooling system. Therefore we can see in the second assumption the energy is proportional to temperature.

The energy saved by IA every time (1 minute) is:

IA Energy saved between t y $t+1$ :

$= |\Delta T_t^{Intern System Server (no-IA)}| - |\Delta T_t^{IA}|$
$= |\Delta T_t^{\textrm{no IA}}| - |\Delta T_t^{\textrm{IA}}|$

Our goal is to save the maximum energy every minute, thus save the maximum total energy for 1 whole simulation year, and finally save the maximum costs on the cooling/heating electricity bill.

Now let’s to define the states, actions and rewards. (You can get more information about Q-learning from here: A Beginners Guide to Q-Learning)

States

The state $s_t$ is a vector that made up of:

Server temperature in time t.
Number users in t.
Data transmission speed in t.

Actions

0: IA cools the server 3ºC (- 3ºC).
1: IA cools the server 1.5ºC (- 1.5ºC).
2: IA makes no difference.
3: IA heats up the server 1.5ºC (+ 1.5ºC).
4: IA heats up the server 3ºC (+ 3ºC).

Rewards

The reward is the energy expended on the server that the AI is saving relative to the server’s intern cooling system (no-IA):

$\textrm{Reward}_t = E_t^{\textrm{no IA}} - E_t^{\textrm{IA}}$

Then:

$Reward_t =$ Saved energy by IA between t and $t+1$ $= E_t^{no IA} - E_t^{IA} = |\Delta T_t^{no IA}| - |\Delta T_t^{IA}|$

2 – Deep Q-Learning algorithm

For each state $s_t$ :

$Q(s_t,a_t)$ is the prediction and we choose $a_t$ with argmax or softmax (https://deepai.org/machine-learning-glossary-and-terms/softmax-layer).
The target value is: $r_t + \gamma \underset{a}{\max}(Q(s_{t+1}, a))$ , where $r_t=R(s_t,a_t) + \gamma \underset{a}{\max}(Q(s_{t+1},a))$ is the reward, and $\gamma$ is the discount factor (https://en.wikipedia.org/wiki/Q-learning#Discount_factor)
Loss error between the prediction and the target is: $\textrm{Loss} = \frac{1}{2} \left( r_t + \gamma \underset{a}{\max}(Q(s_{t+1}, a)) - Q(s_t, a_t) \right)^2 = \frac{1}{2} TD_t(s_t, a_t)^2.$ , where $TD_t(s_t,a_t) = R(s_t,a_t) + \gamma \underset{a}{\max}(Q(s_{t+1},a)) - Q(s_t,a_t)$ . This loss error spreads to net back and weights are update.

Other problem to solve, $s_t$ is almost always highly correlated with $s_{t+1}$ , therefore our system isn’t learning as much as we would like. Let’s consider the last m transitions blocks (m is a big number). This is known as Experience Replay.

Our brain will have 64 neurons in the first layer and 32 neurons in second layer. This neural network takes the environment’s states as inputs and returns the Q-values for each of the 5 actions as outputs. This artificial brain will be trained with a "mean square error" loss (MSE) and an Adam optimizer.

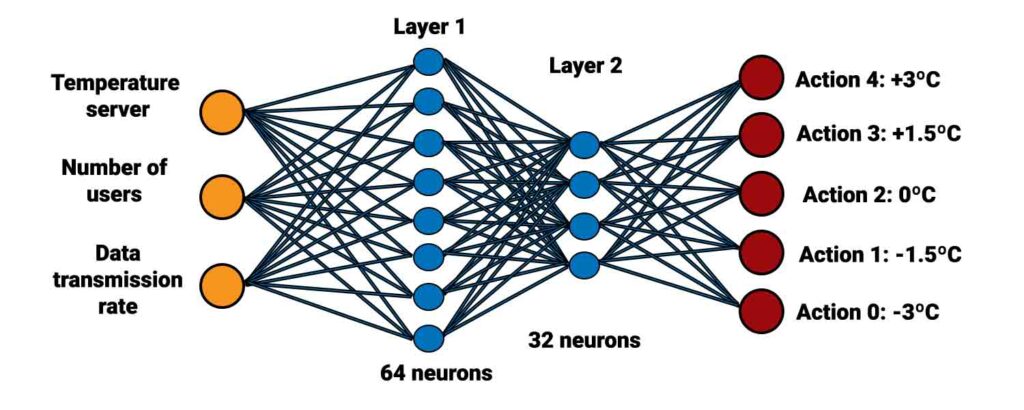
Algorithm steps:

First we need to start the Expereince Replay like a empty list M. Then:

1 – $Q(s_t)$ prediction.

2 – We execute the maximum Q-values acttion: $a_t = \underset{a}{\textrm{argmax}} Q(s_t, a)$ .

3 – We get the Reward: $r_t = E_t^{\textrm{no IA}} - E_t^{\textrm{IA}}$ .

4 – Next state $s_{t+1}$ .

5 – Update Experience Replay memory (M) with $(s_t, a_t, r_t, s_{t+1})$ .

6 – We select a random block transitions $B \subset M$ $(s_{t_B}, a_{t_B}, r_{t_B}, s_{t_B+1})$ , then we get the new predictions, new targets and the new loss error. Finally the error spreads throw the neuronal network with a Stochastic gradient descent and the weights will be update.

Algorithm implementation:

1 – Building the environment.

2 – Builiding the brain.

3 – Deep Reinforcement Learning algorithm.

4 – Training the IA.

5 – Testing the IA.

Environment

We are going to create teh environment into a class called Environment. This class contains 4 methods, the class’s constructor method (init()), a method to update the environment (update_env()(…)), a method to reset the environment (rest(…)) and finnaly a method to give us information about some variables (observe(…)).

– The general structure will be:

# Import libraries
import numpy as np

#Create the class and its methods
class Environment(object):

    def __init__(self, optimal_temp, initial_month, initial_number_users, initial_rate_data):
        ...............
        ...............

    def update_env(self, direction, energy, energy_ai, month):
        ..............
        ..............

        return next_state, reward, game_over

    def reset_env(self, new_month):
        .............
        .............

    def give_env(self):
        ............
        ............

        return current_state, reward, game_over

1 – Introduction and initialization of environment variables and parameters.

 def __init__(self, optimal_temp = (15, 25), initial_month = 0, initial_number_users = 8, initial_rate_data = 80):
        #For example, Average Weather in Köln, Germany (https://en.climate-data.org/europe/germany/north-rhine-westphalia/cologne-76/#:~:text=The%20average%20annual%20temperature%20in,%C2%B0C%20%7C%2050.2%20%C2%B0F.)
        self.monthly_atmospheric_temp = [1.8, 2.5, 6, 9.5, 13.6, 16.7, 18.3, 18.1, 15.1, 10.5, 6.1, 2.9]
        self.initial_month = initial_month
        self.atmospheric_temp = self.monthly_atmospheric_temp[initial_month]
        self.optimal_temp = optimal_temp
        self.min_temp = -25
        self.max_temp = 80
        self.min_number_users = 8
        self.max_number_users = 120
        self.max_update_users = 6
        self.min_rate_data = 20
        self.max_rate_data = 400
        self.max_update_data = 10
        self.initial_number_users = initial_number_users
        self.current_number_users = initial_number_users
        self.initial_rate_data = initial_rate_data
        self.current_rate_data = initial_rate_data
        self.intrinsec_temp = self.atmospheric_temp + 1.3*self.current_number_users+1.3*self.current_rate_data
        self.temp_ai = self.intrinsec_temp
        self.temp_noai = (self.optimal_temp[0]+self.optimal_temp[1])/2.0
        self.total_energy_ai = 0.0
        self.total_energy_noai = 0.0
        self.reward = 0.0
        self.game_over = 0
        self.train = 1

2 – Creating a update environment method after the IA performs an action.

    def update_env(self, direction, energy_ai, month):
        # GETTING THE REWARD

        # Energy spended by cooling system server (no-IA)
        energy_noai = 0
        if(self.temp_noai  < self.optimal_temp[0]):
            energy_noai = self.optimal_temp[0] - self.temp_noai
            self.temp_noai = self.optimal_temp[0]
        elif(self.temp_noai > self.optimal_temp[1]):
            energy_noai = self.temp_noai - self.optimal_temp[1]
            self.temp_noai = self.optimal_temp[1]

        # The Reward
        self.reward = energy_noai - energy_ai
        # Scaled the reward
        self.reward = 1e-3*self.reward

        # GETTING THE NEXT STATE

        # Updating the atmospheric temp
        self.atmospheric_temp = self.monthly_atmospheric_temp[month]
        # Updating the number of users
        self.current_number_users += np.random.randint(-self.max_update_users, self.max_update_users)
        if(self.current_number_users < self.min_number_users):
            self.current_number_users = self.min_number_users
        elif(self.current_number_users > self.max_number_users):
            self.current_number_users = self.max_number_users
        # Updating the current rate data
        self.current_rate_data += np.random.randint(-self.max_update_data, self.max_update_data)
        if(self.current_rate_data < self.min_rate_data):
            self.current_rate_data = self.min_rate_data
        elif(self.current_rate_data > self.max_rate_data):
            self.current_rate_data = self.max_rate_data
        # Intrinsic temperature variation
        past_intrinsic_temp =  self.intrinsec_temp #previous temperature 
        self.intrinsec_temp = self.atmospheric_temp + 1.3*self.current_number_users+1.3*self.current_rate_data
        delta_intrinsec_temperaure = self.intrinsec_temp - past_intrinsic_temp
        # Temperature variation caused by IA
        if(direction==-1): #if temperature down 
            delta_temp_ai = -energy_ai
        elif(direction == 1): #if temperature up
            delta_temp_ai = energy_ai
        # New server temperature when IA is connected
        self.temp_ai += delta_intrinsec_temperaure + delta_temp_ai
        # New server temperature when IA is disabled
        self.temp_noai += delta_intrinsec_temperaure

        # GETTING THE GAME OVER
        if(self.temp_ai < self.min_temp):
            if(self.train == 1):
                self.game_over = 1
            else:
                self.total_energy_ai += self.optimal_temp[0] - self.temp_ai
                self.temp_ai = self.optimal_temp[0]
        if(self.temp_ai > self.max_temp):
            if(self.train == 1):
                self.game_over = 1
            else:
                self.total_energy_ai += self.temp_ai - self.optimal_temp[1]
                self.temp_ai = self.optimal_temp[1]

        # UPDATING THE SCORES

        # Total Energy spends by IA
        self.total_energy_ai += energy_ai
        # Total Energy spends by no-IA (without IA)
        self.total_energy_noai += energy_noai


        # SCALING NEXT STATE 
        scaled_temp_ai = (self.temp_ai - self.min_temp)/(self.max_temp - self.min_temp)
        scaled_number_users = (self.current_number_users - self.min_number_users)/(self.max_number_users - self.min_number_users)
        scaled_rate_data = (self.current_rate_data - self.min_rate_data)/(self.max_rate_data - self.min_rate_data)
        next_state = np.matrix([scaled_temp_ai, scaled_number_users, scaled_rate_data])

        # RETURN NEXT STATE, REWARD AND GAME OVER
        return next_state, self.reward, self.game_over

3 – Creating a reset environment method.

    def reset_env(self, new_month):
        self.atmospheric_temp = self.monthly_atmospheric_temp[new_month]
        self.initial_month = new_month
        self.current_number_users = self.initial_number_users
        self.current_rate_data = self.initial_rate_data
        self.intrinsec_temp = self.atmospheric_temp + 1.3*self.current_number_users+1.3*self.current_rate_data
        self.temp_ai = self.intrinsec_temp
        self.temp_noai = (self.optimal_temp[0]+self.optimal_temp[1])/2.0
        self.total_energy_ai = 0.0
        self.total_energy_noai = 0.0
        self.reward = 0.0
        self.game_over = 0
        self.train = 1

4 – Creating a method who gives us the state, the reward and the end of the game any moment.

    def give_env(self):
        scaled_temp_ai = (self.temp_ai - self.min_temp)/(self.max_temp - self.min_temp)
        scaled_number_users = (self.current_number_users - self.min_number_users)/(self.max_number_users - self.min_number_users)
        scaled_rate_data = (self.current_rate_data - self.min_rate_data)/(self.max_rate_data - self.min_rate_data)
        current_state = np.matrix([scaled_temp_ai, scaled_number_users, scaled_rate_data])

        return current_state, self.reward, self.game_over

The Brain

We are going to build a neuronal network like this:

Import the libraries:

from keras.layers import Input, Dense, Dropout
from keras.models import Model
from keras.optimizers import Adam

Building the brain:

class Brain(object):
	def __init__(self, learning_rate = 0.001, number_actions = 5):
		self.learning_rate = learning_rate

		# INPUT LAYER FORMED BY INPUT STATES
		states = Input(shape = (3,))

		# TWO HIDDEN LAYERS TOTALLY CONNECTED
		x = Dense(units = 64, activation = 'sigmoid')(states)
		x = Dropout(rate = 0.1)(x) #during training in each iteration 10% of neurons will be randomly turned off
		y = Dense(units = 32, activation = 'sigmoid')(x)
		y = Dropout(rate = 0.1)(y) #during training in each iteration 10% of neurons will be randomly turned off

		# OUTPUT LAYER TOTALLY CONNECTED TO THE LAST HIDDEN LAYER
		q_values = Dense(units = number_actions, activation = 'softmax')(y)

		# JOINING KERAS MODEL 
		self.model = Model(inputs = states, outputs = q_values)

		# COMPILING THE MODEL WITH THE MEAN SQUARE ERROR LOSS FUNCTION(MSE) AND THE OPTIMIZER (Adam)
		self.model.compile(loss = 'mse', optimizer = Adam(lr = learning_rate))

Deep Reinforcement Learning Algorithm(DQN)

Import libraries:

import numpy as np

Algorithm Implementation:

class DQN(object):

    # INICIALIZATION DQN PARAMETERS
    def __init__(self, max_memory = 100, discount_factor = 0.9):
        self.memory = list()
        self.max_memory = max_memory
        self.discount_factor = discount_factor #gamma factor

    # BUILDING A EXPERIENCE DELAY MEMORY
    def remember(self, transition, game_over):
        self.memory.append([transition, game_over])
        if len(self.memory) > self.max_memory:
            del self.memory[0]

    # BUILDING A METHOD THAT BUILDS TWO INPUTS AND TARGETS BLOCKS AND EXTRACTING THE MEMORY'S TRANSITIONS
    def get_batch(self, model, batch_size = 10):
        len_memory = len(self.memory)
        num_inputs = self.memory[0][0][0].shape[1]
        num_outputs = model.output_shape[-1]
        inputs = np.zeros((min(batch_size, len_memory), num_inputs))
        targets = np.zeros((min(batch_size, len_memory), num_outputs))
        for i, idx in enumerate(np.random.randint(0, len_memory, size=min(len_memory, batch_size))):
            current_state, action, reward, next_state = self.memory[idx][0] #we want the memory's transition
            game_over = self.memory[idx][1]
            inputs[i] = current_state
            targets[i] = model.predict(current_state)[0]
            Q_sa = np.max(model.predict(next_state)[0])
            if game_over:
                targets[i, action] = reward
            else:
                targets[i, action] = reward + self.discount_factor*Q_sa
        return inputs, targets

Training the IA

Import python libraries and our libraries:

import os
import numpy as np
import random as rn

import environment
import brain
import dqn

Reproducibility seeds setup:

os.environ['PYTHONHASHSEED'] = '0'
np.random.seed(85)
rn.seed(12345)

Parameters:

epsilon = 0.3 #our system will take 30% exploration(action random selection) and 70% explotation
number_actions = 5
direction_boundary = (number_actions -1)/2 #intermediate point (our boundary)
number_epochs = 100
max_memory = 3000
batch_size = 512
temp_step = 1.5

Building the environment with a class object Environment()

env = environment.Environment(optimal_temp = (15.0, 25.0), initial_month = 0, initial_number_users = 18, initial_rate_data = 32)

Building the brain with a class object Brain()

brain = brain.Brain(learning_rate = 0.00001, number_actions = number_actions)

Building DQN model with a class object DQN()

dqn = dqn.DQN(max_memory = max_memory, discount_factor = 0.9)

Choosing training mode

train = True

IA training

env.train = train
model = brain.model
early_stopping = True
patience = 10
best_total_reward = -np.inf
patience_count = 0

if (env.train):
    # STARTING EPOCH BUCLE (1 Epoch = 5 Mouths)
    for epoch in range(1, number_epochs):
        # STARTING ENVIRONMEN VARIABLES AND TRAINING BUCLE
        total_reward = 0
        loss = 0.
        new_month = np.random.randint(0, 12)
        env.reset_env(new_month = new_month)
        game_over = False
        current_state, _, _ = env.give_env() #we only want current_state return from give_env method
        timestep = 0
        # INICIALIZATION TIMESTEPS BUCLE(Timestep = 1 minute) AT ONE EPOCH
        while ((not game_over) and timestep <= 5 * 30 * 24 * 60):
            # RUNNING NEXT ACTION BY EXPLORATION
            if np.random.rand() <= epsilon:
                action = np.random.randint(0, number_actions)
                if (action - direction_boundary < 0):
                    direction = -1
                else:
                    direction = 1
                energy_ai = abs(action - direction_boundary) * temp_step
            
            # RUNNING NEXT ACTION BY EXPLOTATION
            else:
                q_values = model.predict(current_state)
                action = np.argmax(q_values[0])
                if (action - direction_boundary < 0):
                    direction = -1
                else:
                    direction = 1
                energy_ai = abs(action - direction_boundary) * temp_step
               
            # UPDATING ENVIRONMENT AND REACHING NEXT STATE
            next_state, reward, game_over = env.update_env(direction, energy_ai, int(timestep/(30*24*60)))
            total_reward += reward

            # SAVING NEW TRANSITION IN MEMORY
            dqn.remember([current_state, action, reward, next_state], game_over)

            # GETTING INPUTS AND TARGETS BLOCKS
            inputs, targets = dqn.get_batch(model, batch_size)

            # CALCULATING LOOST FUNCTION WITH THE WHOLE INPUT AND TARGET BLOCK
            loss += model.train_on_batch(inputs, targets)
            timestep += 1
            current_state = next_state

        # PRINTING RESULTS AT THE END OF EPOCH
        print("\n")
        print("Epoch: {:03d}/{:03d}.".format(epoch, number_epochs))
        print(" - Total Energy spended by IA: {:.0f} J.".format(env.total_energy_ai))
        print(" - Total Energy spended by no-IA: {:.0f} J.".format(env.total_energy_noai))

        # EARLY STOPPING
        if early_stopping:
            if (total_reward <= best_total_reward):
                patience_count += 1
            else:
                best_total_reward = total_reward
                patience_count = 0

            if patience_count >= patience:
                print("Early method execution.")
                break


        # Saving model for the future
        model.save("model.h5")

Epoch: 001/100.
 - Total Energy spended by IA: 22 J.
 - Total Energy spended by no-IA: 29 J.

Epoch: 002/100.
 - Total Energy spended by IA: 28 J.
 - Total Energy spended by no-IA: 26 J.

Epoch: 003/100.
 - Total Energy spended by IA: 20 J.
 - Total Energy spended by no-IA: 39 J.

Epoch: 004/100.
 - Total Energy spended by IA: 4 J.
 - Total Energy spended by no-IA: 2 J.

Epoch: 005/100.
 - Total Energy spended by IA: 4 J.
 - Total Energy spended by no-IA: 1 J.

Epoch: 006/100.
 - Total Energy spended by IA: 10 J.
 - Total Energy spended by no-IA: 12 J.

Epoch: 007/100.
 - Total Energy spended by IA: 22 J.
 - Total Energy spended by no-IA: 48 J.

Epoch: 008/100.
 - Total Energy spended by IA: 22 J.
 - Total Energy spended by no-IA: 19 J.

Epoch: 009/100.
 - Total Energy spended by IA: 122 J.
 - Total Energy spended by no-IA: 181 J.

Epoch: 010/100.
 - Total Energy spended by IA: 3 J.
 - Total Energy spended by no-IA: 0 J.

Epoch: 011/100.
 - Total Energy spended by IA: 134 J.
 - Total Energy spended by no-IA: 169 J.

Epoch: 012/100.
 - Total Energy spended by IA: 84 J.
 - Total Energy spended by no-IA: 59 J.

Epoch: 013/100.
 - Total Energy spended by IA: 252 J.
 - Total Energy spended by no-IA: 352 J.

Epoch: 014/100.
 - Total Energy spended by IA: 8 J.
 - Total Energy spended by no-IA: 4 J.

Epoch: 015/100.
 - Total Energy spended by IA: 27 J.
 - Total Energy spended by no-IA: 77 J.

Epoch: 016/100.
 - Total Energy spended by IA: 8 J.
 - Total Energy spended by no-IA: 16 J.

Epoch: 017/100.
 - Total Energy spended by IA: 18 J.
 - Total Energy spended by no-IA: 44 J.

Epoch: 018/100.
 - Total Energy spended by IA: 6 J.
 - Total Energy spended by no-IA: 2 J.

Epoch: 019/100.
 - Total Energy spended by IA: 8 J.
 - Total Energy spended by no-IA: 1 J.

Epoch: 020/100.
 - Total Energy spended by IA: 33 J.
 - Total Energy spended by no-IA: 25 J.

Epoch: 021/100.
 - Total Energy spended by IA: 78 J.
 - Total Energy spended by no-IA: 131 J.

Epoch: 022/100.
 - Total Energy spended by IA: 706 J.
 - Total Energy spended by no-IA: 960 J.

Epoch: 023/100.
 - Total Energy spended by IA: 50 J.
 - Total Energy spended by no-IA: 304 J.

Epoch: 024/100.
 - Total Energy spended by IA: 8 J.
 - Total Energy spended by no-IA: 34 J.

Epoch: 025/100.
 - Total Energy spended by IA: 0 J.
 - Total Energy spended by no-IA: 0 J.

Epoch: 026/100.
 - Total Energy spended by IA: 4 J.
 - Total Energy spended by no-IA: 61 J.

Epoch: 027/100.
 - Total Energy spended by IA: 86 J.
 - Total Energy spended by no-IA: 282 J.

Epoch: 028/100.
 - Total Energy spended by IA: 32 J.
 - Total Energy spended by no-IA: 148 J.

Epoch: 029/100.
 - Total Energy spended by IA: 21 J.
 - Total Energy spended by no-IA: 67 J.

Epoch: 030/100.
 - Total Energy spended by IA: 8 J.
 - Total Energy spended by no-IA: 41 J.

Epoch: 031/100.
 - Total Energy spended by IA: 6 J.
 - Total Energy spended by no-IA: 7 J.

Epoch: 032/100.
 - Total Energy spended by IA: 20 J.
 - Total Energy spended by no-IA: 61 J.

Epoch: 033/100.
 - Total Energy spended by IA: 24 J.
 - Total Energy spended by no-IA: 189 J.
Early method execution.

Testing the IA

Import python libraries and our libraries:

import os
import numpy as np
import random as rn
from keras.models import load_model
import environment

STTING UP SEEDS OF REPRODUCIBILITY

os.environ['PYTHONHASHSEED'] = '0'
np.random.seed(85)
rn.seed(12345)

SETTING UP PARAMETERS

number_actions = 5
direction_boundary = (number_actions -1)/2
temp_step = 1.5

BUILDING ENVIERONMENT WITH A CLASS OBJECT ENMIRONMENT()

env = environment.Environment(optimal_temp = (15.0, 25.0), initial_month = 0, initial_number_users = 18, initial_rate_data = 32)

LOADING THE MODEL

model = load_model("model.h5")

CHOOSING THE TRAINING MODEL (=False)

train = False

RUNNING A YEAR SIMULATION (EXPLOTATION)

env.train = train
current_state, _, _ = env.give_env()
for timestep in range(0, 12*30*24*60):
    q_values = model.predict(current_state)
    action = np.argmax(q_values[0])
            
    if (action < direction_boundary):
        direction = -1
    else:
        direction = 1
    energy_ai = abs(action - direction_boundary) * temp_step
    next_state, reward, game_over = env.update_env(direction, energy_ai, int(timestep/(30*24*60)))
    current_state = next_state

PRINTING RESULTS AT THE END OF EPOCH

print("\n")
print("  - Total Energy spended by IA: {:.0f} J.".format(env.total_energy_ai))
print(" - Total Energy spended by no-IA: {:.0f} J.".format(env.total_energy_noai))
print("--------------------------------------------------")
print(" ENERGY SAVED: {:.0f} %.".format(100*(env.total_energy_noai-env.total_energy_ai)/env.total_energy_noai))

 - Total Energy spended by IA: 382928 J.
 - Total Energy spended by no-IA: 1595671 J.
--------------------------------------------------
 ENERGY SAVED: 76 %.

Cutting Data Center Cooling Costs

1 – Boundary Conditions and program operation

How the simulation works:

General operation:

States

Actions

Rewards

2 – Deep Q-Learning algorithm

Algorithm steps:

Algorithm implementation:

Environment

1 – Introduction and initialization of environment variables and parameters.

2 – Creating a update environment method after the IA performs an action.

3 – Creating a reset environment method.

4 – Creating a method who gives us the state, the reward and the end of the game any moment.

The Brain

Import the libraries:

Building the brain:

Deep Reinforcement Learning Algorithm(DQN)

Import libraries:

Algorithm Implementation:

Training the IA

Import python libraries and our libraries:

Reproducibility seeds setup:

Parameters:

Building the environment with a class object Environment()

Building the brain with a class object Brain()

Building DQN model with a class object DQN()

Choosing training mode

IA training

Testing the IA

Import python libraries and our libraries:

STTING UP SEEDS OF REPRODUCIBILITY

SETTING UP PARAMETERS

BUILDING ENVIERONMENT WITH A CLASS OBJECT ENMIRONMENT()

LOADING THE MODEL

CHOOSING THE TRAINING MODEL (=False)

RUNNING A YEAR SIMULATION (EXPLOTATION)

PRINTING RESULTS AT THE END OF EPOCH

Like this: